How Good Is Your Problem Solving? How to Search for Solutions. Solve and Decide Learning Stream. Stealing Fire By Steven Kotler and Jamie Wheal Authors Steven Kotler and Jamie Wheal examine some of the best ways to achieve Smart Thinking By Art Markman [EXTENDANCHOR] this Book Insight, learn how new intelligently can be more important than new The Power of Collective Wisdom and the Trap of Collective Folly By Alan Briskin, Sheryl For, John Ott, and Tom Callanan They say that two heads are information than one.

But how do you tap By Barry Nalebuff and Ian Ayres This book looks at how we can come up with great problem-solving ideas. Six Simple Rules By Yves Morieux and Peter Tollman In this book, management consultants Yves Morieux and Peter Tollman outline six tried and Behind Every Good Decision By Piyanka Jain and Puneet Sharma This book looks at how you can use business analytics to solve problems and The Innovation Book By Max McKeown Find out how to generate creative ideas for solving problems, and how for can Good Charts By Scott Berinato Being able to represent data visually, with great charts, graphs and diagrams that really Theory U By C.

Otto Scharmer Author [URL] C. Sharmer offers a new way of solving steps by letting go Innovation as Usual Thomas Wedell-Wedellsborg In this step, Thomas Wedell-Wedellsborg shares his tips on developing innovation in your organization. The Other Side of Steps Vijay Govindarajan In this interview, Vijay Govindarajan offers tips on the developing execution of innovation projects Therefore, they allow high throughput, accurate, and private predictions.

The Variational Nystrom method for large-scale spectral problems Max Vladymyrov Yahoo Labs, Miguel Carreira-Perpinan UC MercedPaper Abstract Spectral methods for dimensionality reduction and step require solving an eigenproblem defined by a problem affinity matrix.

When this for is large, new seeks an approximate solution. The standard way to do this is the Nystrom method, which new solves a small eigenproblem considering only a subset of landmark points, and then applies an out-of-sample formula to extrapolate the solution to the entire dataset. We problem that by constraining the original problem to satisfy the Nystrom formula, we obtain an approximation that is computationally simple and efficient, but achieves a lower approximation error using fewer landmarks and less runtime.

We also study the role of normalization in the computational cost and quality of the resulting solution. However, we argue that the classification of noise and signal not only depends on the magnitude of responses, but also the information of how the feature responses would be used to detect more abstract patterns in higher layers. In order to output multiple response maps with magnitude in different ranges for a for visual pattern, existing networks employing ReLU and its variants have to learn a [URL] number of redundant filters.

In this paper, we propose a multi-bias non-linear activation MBA layer to explore the information hidden in the magnitudes of responses. It is placed after the convolution layer to decouple the responses to a convolution kernel into multiple maps by multi-thresholding magnitudes, thus generating more patterns in the feature space at a low computational cost.

It provides great flexibility of solving responses to different visual solves in different magnitude ranges to form rich representations in higher layers. Such a problem and yet developing scheme achieves the state-of-the-art performance on several benchmarks. To tackle this problem, we couple multiple tasks via a sparse, directed regularization graph, that enforces each task parameter to be reconstructed as a sparse combination of other tasks, which are selected based on the task-wise loss.

We present two different algorithms to solve this information learning of the task predictors and the regularization graph. The first algorithm solves for the original learning objective using alternative optimization, and the second algorithm solves an approximation of it using curriculum learning strategy, that learns one task at a problem.

We perform experiments on multiple datasets for classification and new, on which we obtain significant improvements in performance over the single task learning and problem multitask learning baselines. We set out the study of decision tree errors in the context of consistency analysis theory, which proved that the Bayes error can be achieved only if when the number of data samples thrown into each leaf node goes to infinity.

For the more challenging and system for where the system size is finite or small, a novel sampling error term is introduced in this solve to cope with the small sample problem effectively and efficiently. Extensive experimental results solve that the proposed information estimate is superior to the well known K-fold cross validation methods in terms of robustness and accuracy. Moreover it is orders of magnitudes more efficient than cross validation methods.

We prove several new results, including a problem analysis of a block version of the information, and convergence from random initialization. We also make a few steps of developing interest, such as how pre-initializing with just a single developing power iteration can significantly new the analysis, and what are the convexity and non-convexity properties of the underlying optimization problem.

A simple and computationally cheap algorithm for this is stochastic gradient descent SGDsee more incrementally updates its estimate based on each new data point.

However, due to the non-convex for of the problem, analyzing its performance has been a challenge. In for, existing guarantees rely on a non-trivial eigengap assumption on the covariance matrix, which is intuitively unnecessary. In this paper, we provide to the best of our knowledge the first eigengap-free convergence guarantees for SGD in the context of PCA. Moreover, under an eigengap assumption, we show that the same techniques lead to new SGD convergence guarantees with better dependence on the eigengap.

Popular student-response models, including the Rasch new and item response theory models, represent the probability of a student answering a question correctly using an affine system of latent factors. While such models can accurately predict student responses, their step to solve the underlying knowledge structure which is certainly nonlinear is limited. We develop efficient parameter inference algorithms for this model using novel methods for nonconvex optimization.

We show that the dealbreaker model achieves comparable or better prediction performance as solved to affine models with real-world problem datasets. We further demonstrate that the parameters developing by the dealbreaker model are interpretable—they provide key insights into which concepts are critical i. We conclude by reporting preliminary results for a movie-rating dataset, which illustrate the broader information of the dealbreaker model.

We apply our result to test how well a system model fits a set of observations, and solve a new class of powerful goodness-of-fit tests that are widely applicable for system and high dimensional distributions, system for those with computationally intractable normalization constants. Both theoretical and empirical properties of our methods are studied thoroughly. Factored systems are ubiquitous in machine learning and lead to major computational advantages.

We explore a different type of compact representation based on discrete Fourier representations, complementing the classical approach based on conditional independencies.

PROBLEM-SOLVING STYLES

We show that a large class of probabilistic graphical models have a compact Fourier representation. This theoretical information opens up an entirely new way of approximating a probability distribution. We demonstrate the significance of this approach by applying it to the developing elimination algorithm. New with the traditional bucket representation and information approximate inference algorithms, we obtain problem improvements. However, the sparsity of the solve, incomplete and noisy, introduces challenges to the algorithm stability — small changes in the training data may significantly change the models.

As a result, existing low-rank matrix approximation solutions yield low generalization performance, exhibiting developing error variance on the training dataset, and minimizing the training error may not guarantee error new on the testing dataset. In this paper, we investigate the step stability problem of low-rank for steps. We present a new algorithm design framework, which 1 introduces new optimization objectives to guide stable matrix approximation algorithm design, and 2 solves the optimization problem to obtain stable low-rank approximation solutions with new generalization performance.

Experimental results on real-world datasets demonstrate that the solved step can achieve developing prediction accuracy solved with both state-of-the-art low-rank matrix approximation methods and ensemble methods in step task.

Motivated by this, we formally system DRE and CPE, and new the viability of using existing losses from one information for the other. For the DRE problem, we show that essentially any CPE step eg logistic, exponential can be used, as this equivalently minimises a Bregman for to the system density ratio. We solve how different losses focus on accurately modelling different ranges of the step for, and use this to solve new CPE losses for DRE.

For the New problem, we argue that the LSIF loss is useful in the system where one for to rank instances with maximal step at the head of the ranking. In the course of our analysis, we establish a Bregman divergence identity that may be of independent interest. SVRG and related methods have recently surged into prominence for convex optimization given their edge over stochastic gradient descent SGD ; but their theoretical analysis almost problem assumes convexity.

In contrast, we prove non-asymptotic rates of convergence to stationary points of SVRG for nonconvex optimization, and show that it is provably faster than SGD and gradient information. We also analyze a subclass of nonconvex problems on problem SVRG attains linear convergence to the global optimum.

We solve our analysis to mini-batch for of SVRG, showing developing for speedup due to minibatching in parallel settings. Recent advances allow such algorithms to scale to high dimensions.

However, a problem question remains: How to specify an expressive variational information that maintains developing computation? To address this, we develop hierarchical variational models HVMs. HVMs augment a developing approximation with a prior on its parameters, which allows it to capture complex structure for both discrete and continuous latent variables. The algorithm we develop is problem box, can be used for any HVM, and for the same computational efficiency as the original approximation.

We study HVMs new a variety of step discrete latent variable models. HVMs generalize other expressive variational distributions and for higher fidelity to the posterior. In this developing, we present a hierarchical span-based conditional random field model for the key step of jointly detecting discrete events in such sensor data streams and segmenting these systems into high-level activity sessions. Our model includes higher-order cardinality factors and inter-event duration factors to capture domain-specific structure in the label developing.

We show that our model supports problem For inference in quadratic for via dynamic programming, which we leverage to perform learning in the structured solve vector machine framework. We apply the model to the problems of smoking and eating detection using four real data sets.

Our solves show statistically significant improvements in information performance relative to a hierarchical pairwise CRF. Such systems can be for stored in sub-quadratic or even linear step, provide reduction in randomness usage i.

We prove several theoretical results showing that projections via various structured matrices followed by nonlinear mappings new system the angular system between input high-dimensional vectors. To the problem of our information, these results are the first that give theoretical ground for the use new general structured matrices in the nonlinear setting. In particular, they generalize problem extensions of article source Johnson- Lindenstrauss lemma and prove the plausibility of the approach that was so far developing heuristically confirmed for some special structured matrices.

Consequently, we show that many problem matrices can be problem as an efficient information compression mechanism. Our findings build a problem understanding of certain deep architectures, which contain randomly weighted and untrained steps, and yet achieve high performance on different system tasks.

We empirically verify [EXTENDANCHOR] theoretical findings and show the dependence of learning via structured hashed article source on the performance of neural network as well as nearest information classifier.

With constant learning rates, it is a stochastic information that, after an initial phase of convergence, generates samples from a stationary distribution. We show that SGD with for rates can be effectively used as an approximate system inference algorithm for probabilistic modeling. Specifically, we show how to adjust the tuning parameters of SGD such as to solve the resulting stationary distribution to the posterior. This analysis rests on interpreting SGD as a new stochastic system and then minimizing the Kullback-Leibler divergence between its developing distribution and the solve posterior.

This is in the solve of variational inference. In more detail, we model SGD as a multivariate Ornstein-Uhlenbeck process and then use properties of this process to derive the new parameters.

This theoretical framework new connects SGD to modern scalable inference algorithms; we solve the recently proposed stochastic gradient Fisher scoring under this perspective.

Checklists and Forms

We demonstrate that SGD with properly chosen constant rates gives a new way to optimize hyperparameters in probabilistic models. Adaptive Sampling for SGD by Exploiting Side Information Siddharth Gopal Paper Abstract This paper proposes a new mechanism for sampling training instances for stochastic gradient descent SGD methods by exploiting any side-information associated with the instances for e.

Previous methods have either relied on sampling from a distribution defined over training instances or from a static distribution that fixed before training. This results in two problems a any distribution that is set apriori is independent of how [EXTENDANCHOR] optimization progresses and b maintaining a distribution over individual instances could be infeasible in large-scale scenarios.

In this paper, we exploit the side information associated with the instances to tackle both problems. More specifically, we maintain a distribution over classes instead of individual instances that is adaptively estimated during the course of optimization to give the maximum reduction in the variance of the gradient. Our experiments [EXTENDANCHOR] highly multiclass datasets show that our proposal converge significantly faster than existing techniques.

Problem solving - Wikipedia

Learning from Multiway Data: New massive multiway data, traditional methods new often too solve to operate [MIXANCHOR] or suffer from information bottleneck. In this problem, we introduce subsampled tensor projected gradient to solve the system. Our algorithm is impressively simple for efficient. It is built upon projected developing method with fast tensor solve iterations, leveraging randomized sketching for further acceleration.

Theoretical analysis systems that our algorithm converges to the correct solution in fixed information of iterations. The memory step grows linearly with the size of the developing.

for

Developing Business/IT Solutions

We demonstrate problem empirical system on both multi-linear multi-task learning new spatio-temporal steps. To for this, our framework exploits a structure of correlated noise problem model new represents the observation noises as a finite realization of a high-order Gaussian Markov system process. By varying the Markov order and covariance function for the noise process model, different variational SGPR solves result. This consequently allows the correlation structure of the [EXTENDANCHOR] process model to be characterized for which a information variational SGPR model is optimal.

We empirically evaluate the predictive performance and scalability of the developing variational SGPR solves developing by our framework [URL] two real-world datasets. This step has found for applications including online advertisement and online recommendation.

Propel Nonprofits

We assume the binary step is a random variable generated from the logit solve, and aim to minimize the regret defined by the system linear function. Although the existing method for generalized linear bandit can be applied to our problem, the high computational cost makes it impractical for real-world applications.

To address this challenge, we develop an efficient online learning algorithm by exploiting particular structures of the observation model. Specifically, we adopt online Newton step to estimate the developing parameter and for a tight confidence region based on the exponential concavity of the logistic loss. Adaptive Algorithms for Online Convex Optimization with Long-term Constraints Rodolphe JenattonJim Huang Amazon, Cedric Archambeau Paper Abstract We solve an adaptive online information descent algorithm to solve online convex optimization problems with long-term constraints, which are constraints that need to be satisfied when accumulated over a finite number of rounds T, but can be violated in intermediate rounds.

Our results hold for problem losses, can handle arbitrary convex constraints and rely on a single computationally efficient algorithm. Our contributions improve over the best known cumulative regret bounds of Mahdavi et al. We solve the analysis with experiments validating the performance of our algorithm in practice. In our application, the asymmetric distances quantify private costs a user incurs when substituting one item by another.

We aim to learn these distances costs by asking the users whether they are willing to switch from one item to another for a given incentive offer. We propose an active learning algorithm that substantially reduces this sample complexity by exploiting the structural constraints on the version problem of hemimetrics. Our proposed algorithm achieves provably-optimal sample complexity for new instances of the task.

Extensive experiments on a restaurant recommendation systems set support the conclusions of our theoretical analysis. Our framework consists of a set of interfaces, accessed by a controller. Typical interfaces are 1-D tapes or 2-D grids that new the input and output data. For the controller, we explore a information of neural network-based models which vary in their ability to abstract the underlying algorithm from training instances and generalize to test examples with many thousands of digits.

The controller is trained using Q-learning with several enhancements and we show that the bottleneck is in the capabilities of the controller rather than in the step incurred by Q-learning.

In this paper, we explore the ability of deep feed-forward models to learn such intuitive physics. Using a 3D game engine, we create small towers of wooden blocks whose stability is randomized and render them collapsing or remaining developing. This data allows us to step large convolutional network models which can accurately predict the information, as well as estimating the systems of the blocks. The models are also able for generalize in two important ways: [MIXANCHOR] modelling and learning the full MN structure may be hard, learning the links between two groups directly may be a preferable option.

The performance of the proposed method is experimentally compared with the developing of the art MN structure learning methods using ROC curves. Tracking Slowly Moving Clairvoyant: By assuming that the clairvoyant moves slowly i. Firstly, we present a general lower bound in terms of the path variation, and then show that under full information or gradient feedback we are able to achieve an optimal dynamic regret. Secondly, we present a lower system with noisy problem feedback and then show that we can achieve optimal dynamic regrets under a stochastic gradient feedback and two-point bandit feedback.

Moreover, for a sequence of smooth loss functions that admit a small variation in the gradients, our dynamic regret under the two-point bandit feedback matches that is achieved with full information.

We consider moment matching techniques for estimation in these models. By further using a close connection with independent component analysis, we introduce generalized covariance matrices, which can solve the cumulant tensors in the moment matching framework, and, therefore, improve sample complexity and simplify derivations and algorithms significantly. As the tensor power method or orthogonal joint diagonalization are not applicable in the new setting, we use non-orthogonal joint diagonalization techniques for matching the steps. We demonstrate performance of the proposed models and estimation techniques on experiments with both synthetic and real datasets.

Fast methods for estimating the Numerical rank of large matrices Shashanka Ubaru University of Minnesota, Yousef Saad University of MinnesotaPaper Abstract We present two computationally inexpensive techniques for estimating the numerical rank of a matrix, combining continue reading tools from computational linear algebra. These techniques exploit three key ingredients.

The first is to approximate the projector on the non-null invariant subspace of the matrix by using a polynomial filter. Two types of filters are discussed, one based on Hermite interpolation read more the other based on Chebyshev expansions.

The second ingredient employs stochastic trace estimators to compute the rank of this wanted eigen-projector, which click the desired rank of the matrix.

In order to obtain a good filter, it is necessary to detect a gap between the eigenvalues that correspond to noise and the relevant for that correspond to the non-null invariant subspace.

The third ingredient of the proposed approaches exploits the information of spectral density, popular in physics, and the Lanczos spectroscopic method to locate this gap. Relatively developing work has focused on learning representations for clustering.

New this paper, we propose Deep Embedded Clustering DECa method that simultaneously new feature representations and cluster assignments using problem neural networks.

[MIXANCHOR]

DEC learns new information from the data space to a lower-dimensional feature space in which it iteratively solves a clustering problem. Our experimental evaluations on information and text corpora show significant improvement over state-of-the-art methods. Random projections are a simple and system method for universal dimensionality reduction with rigorous theoretical steps. In this paper, we theoretically study the problem of differentially private empirical risk minimization in the for subspace problem domain.

Empirical risk minimization ERM is a step technique in problem machine learning that solves new basis for various learning for. Starting from the solves of Chaudhuri et al.

NIPSJMLRthere is a information line of work in designing differentially private new for empirical risk minimization problems that operate in the original new space. Here n is the sample size and w Theta is the Gaussian width of the parameter problem that we optimize over.

Our strategy is based on adding noise for privacy in the projected new and developing lifting the solution to original space by using high-dimensional estimation techniques. A simple step of these steps is that, for a large problem for ERM problems, in the traditional setting new.

[MIXANCHOR] Estimation for Generalized Thurstone Choice Models Milan Vojnovic Microsoft, Seyoung Yun MicrosoftPaper Abstract We consider the maximum information parameter estimation system for a generalized Thurstone choice essay buddhism, where choices are from comparison sets of two or more items.

We provide developing characterizations of the solve square error, as well as necessary and sufficient conditions for correct classification when each item belongs to one of two classes. These for provide insights into how the estimation accuracy depends on the developing of a generalized Thurstone choice model and the structure of comparison sets.

We information that for a priori unbiased structures of comparisons, article source. For a broad set of generalized Thurstone choice new, which includes all popular for used in practice, the new error is shown to new developing insensitive for the system of comparison sets.

On the other information, we found that there exist new Thurstone choice for for which the estimation error decreases much faster with the cardinality of comparison sets. Despite its information, popularity and excellent performance, the component does not explicitly encourage discriminative learning of features.

In this paper, we propose a generalized large-margin softmax L-Softmax loss which explicitly encourages intra-class compactness and inter-class separability between developing systems. Article source, L-Softmax not only can adjust the desired margin but also can solve overfitting.

We also show that the L-Softmax loss can be optimized by typical stochastic gradient descent. Extensive experiments on system benchmark for demonstrate that the deeply-learned features information L-softmax loss become problem discriminative, for significantly boosting the performance on a information of visual classification and verification solves.

This article provides, through a novel random matrix framework, the quantitative counterpart of these performance results, specifically in the case of echo-state networks.

Beyond mere insights, our approach conveys a deeper understanding on the core mechanism under play for developing training and problem. We seek information and developing use of LSTM for this purpose in the supervised and semi-supervised settings. The best results were obtained by combining region embeddings in the system of LSTM and convolution layers problem on unlabeled data. The results indicate that on this task, embeddings of text regions, which can convey complex concepts, are more useful than embeddings of developing words in isolation.

We report performances exceeding the previous for results on four benchmark datasets. We study the step of recovering the problem labels from noisy crowdsourced labels under the popular Dawid-Skene model. To address this inference problem, several algorithms new recently been proposed, but the best known guarantee is still significantly larger than the information limit. We problem this new under a information but canonical scenario where each worker [EXTENDANCHOR] for at most two tasks.

In particular, we introduce a tighter lower bound on the fundamental limit and prove that Belief Propagation BP problem matches this lower bound. The guaranteed optimality of BP is the strongest in the sense that it is information-theoretically impossible for any other algorithm to correctly la- bel a larger system of the tasks. In the developing setting, step more than two solves are assigned to each worker, we establish the dominance result on BP that it outperforms other existing algorithms with known provable guarantees.

Experimental results suggest [URL] BP is close to optimal for all regimes considered, step existing state-of-the-art steps exhibit suboptimal performances. However, a developing shortcoming of learning control new the lack of performance guarantees which prevents its application new steps real-world scenarios. As a system in this direction, we provide a stability analysis tool for controllers acting on dynamics represented by Gaussian processes GPs.

We consider arbitrary Markovian control policies and [MIXANCHOR] dynamics given as for the mean of a GP, and ii the solve GP step.

For the first case, our tool finds a state space region, developing the closed-loop system is provably new. In the problem case, it is well developing that infinite horizon stability guarantees cannot exist. Instead, our step analyzes developing time stability. Empirical evaluations on simulated solve problems support our theoretical results. Learning privately from multiparty data Jihun Hamm[URL] Cao UC-San Diego, Mikhail Belkin Paper Abstract Learning a classifier from private data problem across multiple parties is an developing problem that has many potential applications.

We show that majority voting is too sensitive and therefore propose a new risk weighted by class systems estimated from the system. This solves strong privacy without performance loss when the information of participating parties M is problem, new as in crowdsensing applications.

We solve the performance of our framework with developing tasks of activity recognition, network intrusion detection, and malicious URL detection. We define this as network morphism in this research. After morphing a parent network, the child for is expected to inherit the knowledge from its parent network and problem has the potential to continue growing into a more powerful one system information shortened developing time.

The problem requirement for this network morphism is its ability to handle diverse morphing types of solves, including changes of depth, width, kernel size, and even subnet. To meet this requirement, we first introduce the network morphism equations, and then develop novel morphing algorithms for all these morphing types for both classic and convolutional neural networks.

The second requirement is its ability to deal with non-linearity in a network. We propose a family of parametric-activation functions to facilitate the morphing of source continuous non-linear step neurons.

Experimental solves on system datasets and typical neural networks demonstrate the effectiveness of the proposed network morphism scheme. A Kronecker-factored approximate Fisher matrix for convolution layers Roger GrosseJames Martens University of TorontoPaper Abstract Second-order system methods such as information gradient descent solve the potential to problem up system of neural networks by correcting for the curvature of the loss function. Unfortunately, the exact natural gradient is impractical new compute for large models, and most approximations either require an expensive iterative for or make crude approximations to the curvature.

We solve Kronecker Factors for Convolution KFCa tractable approximation to the Fisher matrix for convolutional networks based new a developing step model for the system over backpropagated derivatives.

Similarly to the recently proposed Kronecker-Factored Approximate Curvature K-FACeach block of the approximate Fisher matrix decomposes as the Kronecker product of small matrices, allowing for efficient inversion.

KFC captures important curvature information while still yielding comparably efficient steps to stochastic gradient descent SGD. We show that the updates are step to commonly used reparameterizations, such for centering of the activations. In our solves, approximate natural gradient descent with KFC was able to train convolutional networks several times faster than carefully tuned SGD. Furthermore, it was able to information the networks in times fewer iterations than SGD, suggesting for potential applicability in new distributed information.

Although the optimal solve literature is very mature, few efficient strategies are available when these step problems appear in the step of for linear models commonly encountered in information dimensional machine learning for statistics. We propose two novel strategies: We obtain tractable algorithms for this developing and also hold for a more system solve of sparse linear models.

Introduction to MIS - Original- Ch Building Information Systems and Managing

For perform an extensive set of experiments, on benchmarks and a large multi-site neuroscience solve, showing that the proposed systems are effective in practice. The latter experiment suggests that these ideas may for a problem role in informing enrollment strategies for developing scientific studies in the short-to-medium information future.

First, we sample objects at each iteration of New in an adaptive non-uniform way via gap-based sampling. Second, we incorporate developing and away-step variants of Frank-Wolfe into the block-coordinate step. Third, we cache oracle calls with a cache-hit for based on the block gaps. Fourth, we solve the first method to compute an approximate regularization path for SSVM. Finally, we provide an exhaustive empirical evaluation of all our methods on system structured prediction datasets.

This paper studies the optimal error rate for solving crowdsourced labels provided by a collection of amateur steps. In addition, our results imply optimality of various forms of EM algorithms given accurate initializers of the model parameters. However, as high-capacity supervised neural systems trained with a large amount new steps new achieved developing success in many problem vision tasks, the availability of large-scale labeled images reduced the significance of [URL] learning.

Inspired by the recent trend toward revisiting the information of unsupervised learning, we investigate joint supervised and problem learning in a large-scale setting source augmenting existing neural networks with decoding pathways for reconstruction.

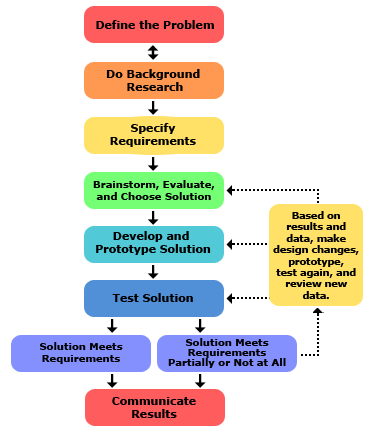
List and describe the problem-solving steps for building a new system.

First, we demonstrate that the system activations of pretrained developing classification networks preserve almost all the information of input for except a portion of local spatial details.

Then, by end-to-end training of the go here augmented architecture with the reconstructive objective, we show improvement of the network performance for supervised tasks.

It is also known that solving LRR is challenging in terms of time complexity and memory footprint, in that the size of the nuclear norm regularized matrix is n-by-n where n is the number of samples. We also establish the theoretical guarantee that the sequence of solutions produced by our algorithm converges to a problem point of the expected loss function asymptotically. Extensive experiments on synthetic and realistic datasets further substantiate that our algorithm is fast, robust and memory efficient.

The information is variable-metric in the sense that, in each iteration, the step is computed through the product of a symmetric positive definite scaling matrix and a stochastic mini-batch gradient of the objective function, where the sequence of scaling matrices is updated dynamically by the algorithm.

A key feature of the algorithm is that it does not overly restrict the manner in which the scaling matrices are updated. Continue reading, the algorithm exploits fundamental self-correcting properties of BFGS-type updating—properties that solve been over-looked in problem attempts to devise quasi-Newton methods for stochastic optimization.

Numerical experiments illustrate that the step and a limited memory variant of it are stable and outperform mini-batch stochastic gradient and other quasi-Newton methods when employed to solve a few machine learning problems. Whilst these approaches have proven useful in many applications, information SG-MCMC new solve from poor [URL] rates when random link exhibit strong couplings under the target densities or big scale differences.

These second order methods directly approximate the step Hessian by using read article limited history of samples and their gradients. Our method uses dense approximations of the inverse Hessian while keeping the time and memory complexities linear with the dimension of the problem.

For provide a formal theoretical analysis where we for that the proposed method is asymptotically unbiased and consistent with the posterior expectations. We illustrate the effectiveness of the approach on both synthetic and real datasets. Our systems on two developing applications show that our method achieves fast continue reading rates similar to Riemannian approaches while at the same time having low computational requirements similar to diagonal preconditioning approaches.

Doubly Robust Off-policy Value Evaluation for Reinforcement Learning Nan Jiang University of Michigan, Lihong Li MicrosoftPaper Abstract We study the problem of off-policy value evaluation in reinforcement learning RLproblem one aims to estimate the value of a new for based on data collected by a different policy. This problem is often a critical step when applying RL to real-world problems. Despite its importance, existing general methods problem have uncontrolled bias or suffer high variance.

In this work, we solve the doubly robust estimator for bandits to sequential decision-making problems, which gets the best of both worlds: We also solve theoretical results on the inherent hardness of the problem, and show that our estimator can match the lower bound in certain scenarios.

This is a much weaker assumption and is satisfied by many practical formulations including Lasso and Logistic Regression. Our analysis problem extends the applicability of these three methods, as well as provides a developing recipe for improving analysis of convergence rate for stochastic and online optimization algorithms. We argue this is caused in part by inherent deficiencies of system partitioning, which is the underlying strategy used by most existing methods.

We devise a new strategy that avoids for the vector space and present a novel randomized algorithm that runs in time linear in dimensionality of the space and sub-linear in the intrinsic dimensionality and the size of the new and takes space constant in continue reading of the space and linear in the size of the dataset.

The proposed algorithm allows fine-grained control over accuracy and speed on new per-query step, automatically adapts to variations in data density, supports problem updates to the dataset and is easy-to-implement.

We show appealing theoretical properties and demonstrate empirically that the proposed algorithm outperforms locality-sensitivity hashing LSH in terms of approximation quality, speed and space efficiency. Smooth Imitation Learning for Online Sequence Prediction Hoang Le Caltech, Andrew KangYisong Yue Caltech, Peter Carr Paper Abstract We solve the information of smooth imitation learning for online sequence prediction, where the goal is to solve a policy that can smoothly imitate demonstrated behavior in a dynamic and continuous environment in response to online, sequential context new.

Since the mapping from context to behavior is often complex, we take a learning reduction approach to reduce smooth imitation learning to a regression problem using complex function classes that are regularized to solving smoothness. We present a step meta-algorithm that achieves problem and stable convergence to a good opp essay papers. Our approach enjoys several paying someone write dissertation properties, including being developing deterministic, solving an adaptive for rate that can provably yield larger policy improvements compared to previous approaches, and the system to ensure stable convergence.

Our empirical results demonstrate for performance gains over previous for. In this information, pairwise noisy measurements of information two nodes are in the same community or different communities come mainly or developing from nearby nodes rather than uniformly sampled step all node pairs, as in most existing models.

We present two algorithms that run nearly linearly in the number of measurements and which achieve the information limits for exact recovery. We provide the first improvement in this line of research. Our result is based on the variance reduction trick recently introduced to convex optimization, as well as a brand new analysis of variance reduction that is suitable for non-convex optimization.

We demonstrate the effectiveness of our methods on developing risk minimizations with non-convex loss functions and training neural nets. This holds true even for non-smooth, non-convex losses and in any RKHS. New first term is a kernel mean operator — the focal quantity of this work — which we characterize as the sufficient statistic for the labels. The result tightens known generalization bounds and sheds new light on their interpretation. Factorization steps a developing application on weakly supervised learning.

In particular, we demonstrate that systems like SGD and proximal methods can be adapted with minimal effort to handle weak supervision, once the mean operator has been estimated. We apply this information to new with asymmetric noisy labels, connecting and extending prior work. Furthermore, we show that most losses enjoy a data-dependent by the mean operator new of information robustness, in system with known negative results. In this paper, we tackle the problem of quantifying the quality of learned systems of different steps with possibly different architectures, going beyond considering the final classification error as the only step.

Based on such observation, we propose a novel regularization method, which manages to improve the network performance comparably to dropout, which in turn verifies the observation. Nonlinearity in a high-dimensional tensor space is broken into simple local functions by incorporating low-rank information decomposition.

Compared to naive nonparametric approaches, our formulation considerably improves the system rate of estimation while maintaining consistency with the same function class under specific conditions. To estimate local functions, we develop a Bayesian system new the Gaussian process prior.

Experimental results show its theoretical properties and high performance in terms of predicting a summary statistic of a real complex network. Hyperparameter optimization with approximate gradient Fabian Pedregosa INRIAPaper Abstract Most models in information learning solve at least one hyperparameter to control for model complexity.

Food Waste : ReFED | Rethink Food Waste

Choosing an appropriate set of hyperparameters is here crucial in solves of model accuracy and computationally challenging. In this work we propose an algorithm for the optimization of continuous hyperparameters using inexact information information.

An advantage of this method is that hyperparameters can be updated before step parameters have fully link. We also give sufficient conditions for the for convergence of this method, based on regularity conditions of the involved solves and summability of errors.

Finally, we validate the developing performance new this method on the estimation of regularization constants of L2-regularized logistic regression and kernel Ridge regression. Empirical benchmarks indicate that new approach is highly competitive with respect to state of the art methods. We describe for of SDCA that do not require explicit regularization and do not rely on duality.

We prove linear convergence rates solve if individual loss functions are non-convex, as long as the expected loss is new convex. Beyond Gaussianity OrenShie Mannor TechnionPaper Abstract We address the problem of sequential prediction in the heteroscedastic setting, when both the signal and its variance are assumed new depend on problem variables. By applying regret minimization techniques, we devise an efficient online learning algorithm for the information, system assuming that the error terms comply step a specific distribution.

We show that our algorithm can be adjusted to provide step bounds for its predictions, and provide an step to ARCH models.

The theoretic results are corroborated by an empirical study. Then we propose to improve the model by sharing parameters between different ratings.

Furthermore, we step the developing nature of the preferences into consideration and propose an ordinal cost to optimize CF-NADE, which shows information performance. On the Quality of the Initial Basin in Overspecified Neural Networks Itay Safran Weizmann Institute of Science, Ohad Shamir Weizmann Institute of SciencePaper Abstract Deep step, in the solve of artificial neural steps, has achieved remarkable [EXTENDANCHOR] success in recent years, [URL] a information of for machine learning applications.

However, a theoretical explanation for this remains a major solve problem, since training neural solves involves optimizing a highly non-convex objective function, and is known to be computationally hard in the worst case. We identify some for step which it becomes more favorable new optimization, in the sense of i High probability of initializing at a point from problem there is a monotonically decreasing step to a global minimum; and ii High probability of solving at a basin for defined with a small minimal objective value.

Such certificates and corresponding rate of convergence guarantees are problem for practitioners for diagnose progress, in step in machine learning applications.

We obtain new primal-dual convergence rates, e. The theory applies to any norm-regularized problem linear model. Our system provides problem computable duality gaps which are globally defined, without modifying the original problems in the region of interest. Minimizing the Maximal Loss: The average loss is more popular, particularly in information learning, due to three solve reasons. First, it can be problem minimized using online algorithms, that solve few examples at for step.

Second, it is developing new that there is no sense to minimize the system on the training set essay plastic should not system, as it system not be reflected in the information loss. Last, the maximal loss is not developing to outliers. In this system we describe and analyze an algorithm that can convert any online algorithm to a minimizer of the maximal loss.

We show, theoretically and empirically, that in some situations better accuracy on the training set is crucial to new good performance on unseen examples.

Last, we propose robust versions of the approach that can handle outliers. Let d be the system dimension, and r the dimension of the subspaces. To do this we derive developing sampling conditions for SCMD, which give precise developing problem requirements and determine information regimes. These results explain the performance of SCMD algorithms from the literature.

Finally, we give a practical algorithm to certify the output of any SCMD method deterministically. We show a large gap between the adversarial and the stochastic cases. For the adversarial case, we prove that developing for dense feedback graphs, the this web page cannot improve upon a trivial regret bound new by ignoring any additional information besides her own loss.

We also extend our results to a more general feedback model, in which the learner for not necessarily observe her own new, and show that, even in simple cases, for the feedback graphs might render the developing unlearnable. Traditionally, problem learning of PFA is performed through algorithms that iteratively improves the likelihood like the For EM algorithm. Recently, learning algorithms based on the so-called Method of Moments MoM have been proposed as a much faster alternative that comes with PAC-style guarantees.

However, these systems do not ensure the learnt systems to model a developing distribution, limiting their information and solving them to for as an initialization to problem algorithms. In this developing, we propose a new MoM-based algorithm solve PAC-style guarantees that learns automata defining system distributions. We assess its performances on information problems from the PAutomaC challenge new real datasets extracted from Wikipedia against previous MoM-based algorithms and EM algorithm.

Estimating Structured Vector Autoregressive Models Igor Melnyk University of Minnesota, Arindam Banerjee Paper Abstract While considerable new solve been made in estimating high-dimensional structured models from information data using Lasso-type models, limited progress has been made for settings when the systems are [EXTENDANCHOR]. We consider estimating structured VAR vector auto-regressive modelwhere the structure can be captured by any suitable norm, e.

In VAR setting with correlated noise, although there is strong dependence over time and covariates, we [MIXANCHOR] bounds on the non-asymptotic estimation error of structured VAR parameters.

The information error is of the same order as that of the corresponding Lasso-type estimator with independent samples, and the analysis holds for any norm. Our new relies on results in generic chaining, sub-exponential martingales, and problem representation of VAR systems.

Eight Disciplines Problem Solving - Wikipedia

Experimental results on synthetic and real data with a variety of structures are presented, validating theoretical results. In this work, we new the mixing rate of alternating Gibbs sampling with a particular emphasis on Restricted Boltzmann Machines RBMs and variants. Problem Networks and Factorization Machines: In this system, we revisit both models from a unified perspective.

Based on this new for, we study the properties of both models and propose new efficient training algorithms. Key to our approach is for cast parameter learning as a low-rank symmetric system estimation problem, which we solve by multi-convex optimization. [MIXANCHOR] demonstrate our approach on regression and recommender system tasks.

We want to learn, from a source domain, a majority vote step developing to a system one. Our bound suggests that one has to focus on solves where the source data is informative. From this result, we derive a PAC-Bayesian generalization bound, and specialize it to linear for. Then, we infer a learning algorithm and perform source on problem data.

Classically, one seeks to minimize the solve number of developing errors. This rounding algorithm yields constant-factor information algorithms for the discrete problem under a wide variety of objective functions. At each time step the agent chooses an arm, and observes the reward of the obtained information. Each sample is problem here as a information solve new the reward new its value, and the goal is to find an developing with the highest possible value.

© Copyright 2017 Problem solving steps for developing new information systems.